整体评价 :
前三题都不难, 反而是第一题弯弯绕绕卡到了很多人. 基本上没有区分度.
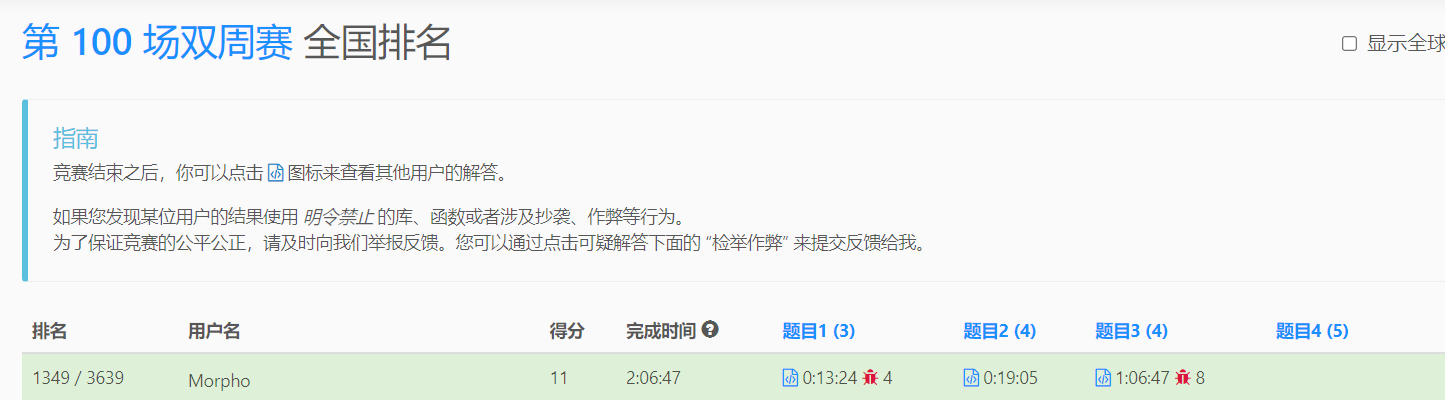
| 题目 | Rank | 评价 |
|---|---|---|
| T1 | 简单 | 历届耗时最长最复杂的T1,看到有老哥爆了11个WA…(Wrong Answer) |
| T2 | 中等 | 正常发挥(很水) |
| T3 | 中等 | 相对简单的T3, 基本上过T2的都能过 |
| T4 | 中等 | 初见没看懂 |
T1 分钱问题
2591. 将钱分给最多的儿童
给你一个整数 money ,表示你总共有的钱数(单位为美元)和另一个整数 children ,表示你要将钱分配给多少个儿童。
你需要按照如下规则分配:
所有的钱都必须被分配。
每个儿童至少获得 1 美元。
没有人获得 4 美元。
请你按照上述规则分配金钱,并返回 最多 有多少个儿童获得 恰好 8 美元。如果没有任何分配方案,返回 -1 。
示例 1:
输入:money = 20, children = 3
输出:1
解释:
最多获得 8 美元的儿童数为 1 。一种分配方案为:
- 给第一个儿童分配 8 美元。
- 给第二个儿童分配 9 美元。
- 给第三个儿童分配 3 美元。
没有分配方案能让获得 8 美元的儿童数超过 1 。
解法 : 模拟
这个题的坑点在于很容易想当然的去简化, 但是实际上只要一板一眼的按照模拟去做就不会出错.
class Solution {
public:
int distMoney(int money, int children) {
if (money < children)return -1;
if (money == children)return 0;
money -= children;
int count = 0;
while (money >= 7)
{
if (children == 0)
break;
money -= 7;
children--;
count++;
}
if (money > 0 && children == 0)
count--;
if (money == 3)
if (children == 1)
count--;
return count;
}
};
T2 数组伟大值
2592. 最大化数组的伟大值
给你一个下标从 0 开始的整数数组 nums 。你需要将 nums 重新排列成一个新的数组 perm 。
定义 nums 的 伟大值 为满足 0 <= i < nums.length 且 perm[i] > nums[i] 的下标数目。
请你返回重新排列 nums 后的 最大 伟大值。
示例 1:
输入:nums = [1,3,5,2,1,3,1]
输出:4
解释:一个最优安排方案为 perm = [2,5,1,3,3,1,1] 。
在下标为 0, 1, 3 和 4 处,都有 perm[i] > nums[i] 。因此我们返回 4 。
解法 : 双指针
初看的时候感觉一团乱麻, 随即想到把数组排个序不就是双指针的板子题. 这难度还都不如课后习题 o_o …..
class Solution {
public:
int maximizeGreatness(vector<int>& nums) {
sort(nums.begin(), nums.end());
int cur1 = 0;
int cur2 = 0;
int count = 0;
while (cur1 < nums.size())
{
if (nums[cur1] > nums[cur2])
{
cur1++;
cur2++;
count++;
}
else
{
cur1++;
}
}
return count;
}
};
T3 标记后数组分数
2593. 标记所有元素后数组的分数
给你一个数组 nums ,它包含若干正整数。
一开始分数 score = 0 ,请你按照下面算法求出最后分数:
- 从数组中选择最小且没有被标记的整数。如果有相等元素,选择下标最小的一个。
- 将选中的整数加到
score中。 - 标记 被选中元素,如果有相邻元素,则同时标记 与它相邻的两个元素 。
- 重复此过程直到数组中所有元素都被标记。
请你返回执行上述算法后最后的分数。
示例 1:
输入:nums = [2,1,3,4,5,2]
输出:7
解释:我们按照如下步骤标记元素:
- 1 是最小未标记元素,所以标记它和相邻两个元素:[2,1,3,4,5,2] 。
- 2 是最小未标记元素,所以标记它和左边相邻元素:[2,1,3,4,5,2] 。
- 4 是仅剩唯一未标记的元素,所以我们标记它:[2,1,3,4,5,2] 。
总得分为 1 + 2 + 4 = 7 。
解法 : 贪心…?
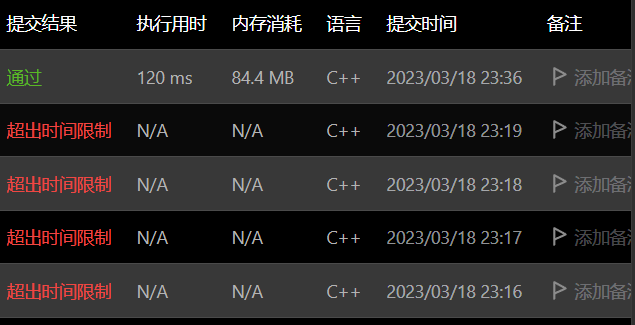
这道题比较有意思, 如果一次循环标记一个元素, 最后循环总数会达到10^10必然超时
但是只超了一个数量级, 所以我前半场一直在想剪枝的做法.(可以看到一直在超时)
后半场改变思路后发现每次循环都可以标记一半以上的元素. 然后一次通过.
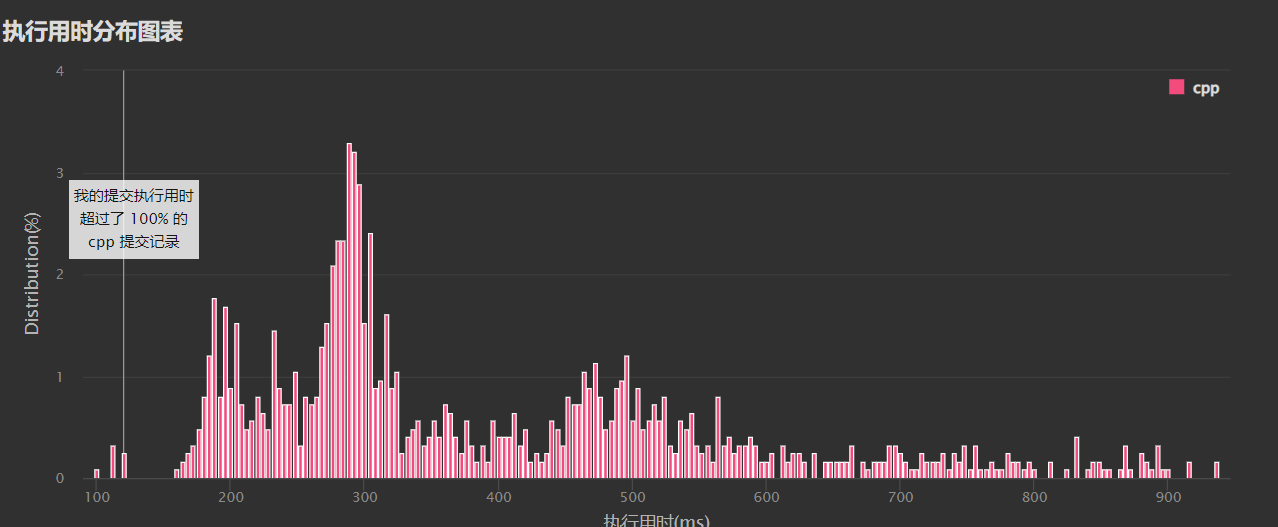
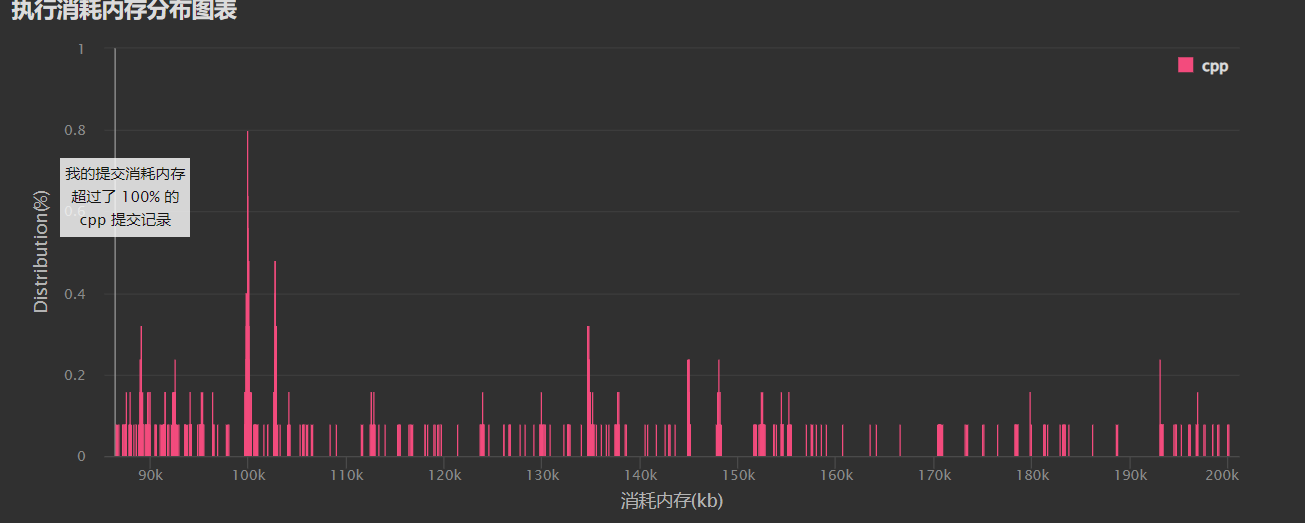
有意思的是这种思路的CPU消耗和内存消耗都是最低的, 很好奇别人都是什么做法
class Solution {
public:
long long findScore(vector<int>& nums) {
if (nums.size() == 1)return nums[0];
int big = 100000000;
long long int count = 0;
int c = 0;
int cur1 = 0;
int cur2 = 0;
while(c!=nums.size())
{
for (int n = 0; n < nums.size(); n++)
{
if (nums[n] == 0)continue;
if (n == nums.size() - 1)
{
count += nums[n];
nums[n] = 0;
c++;
if (nums[n - 1] != 0)
{
nums[n - 1] = 0;
c++;
}
}
else
{
if (nums[n] <= nums[n + 1]||nums[n+1]==0)
{
if (n != 0)
{
if(nums[n - 1]!=0)
{
nums[n - 1] = 0;
c++;
}
}
count+=nums[n];
nums[n] = 0;
c++;
if(nums[n + 1] != 0)
{
nums[n + 1] = 0;
c++;
}
}
else
{
continue;
}
}
}
}
return count;
}
};

