基于OpenCV-C++的n维波函数坍缩算法的实现

2维波函数坍缩算法
openCV环境搭建
素材来源

一 , 复现效果

1.

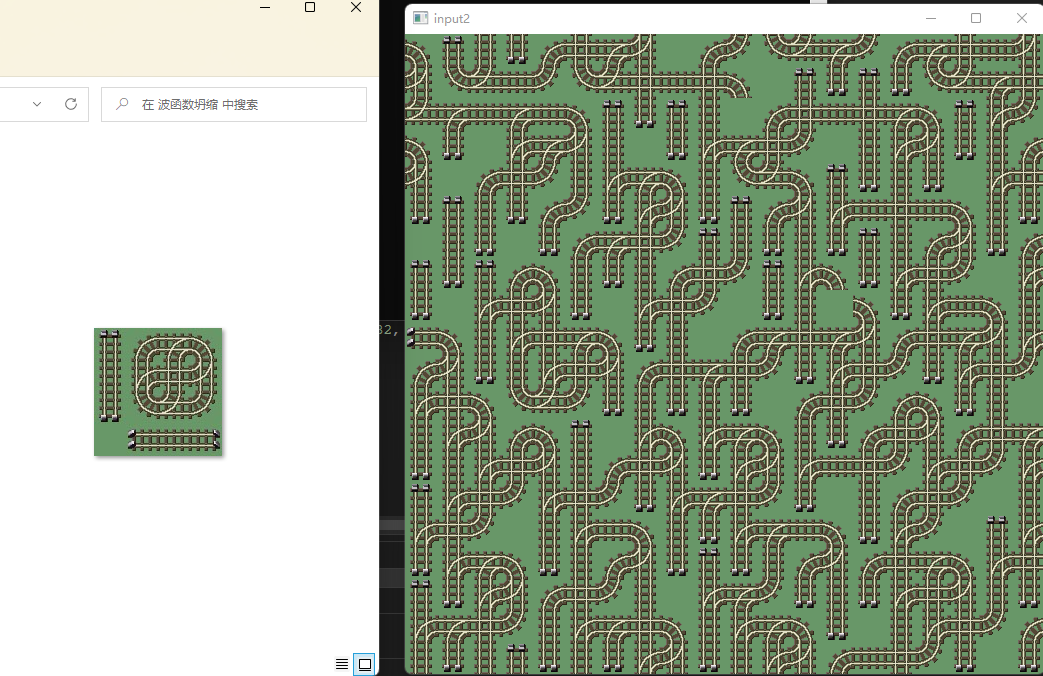
2.

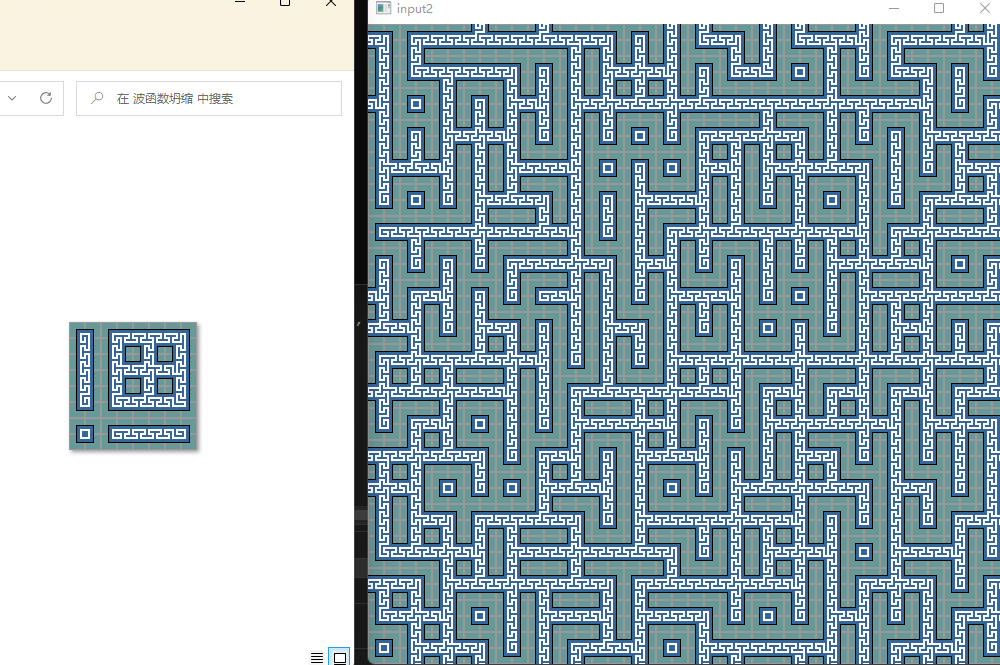
3.

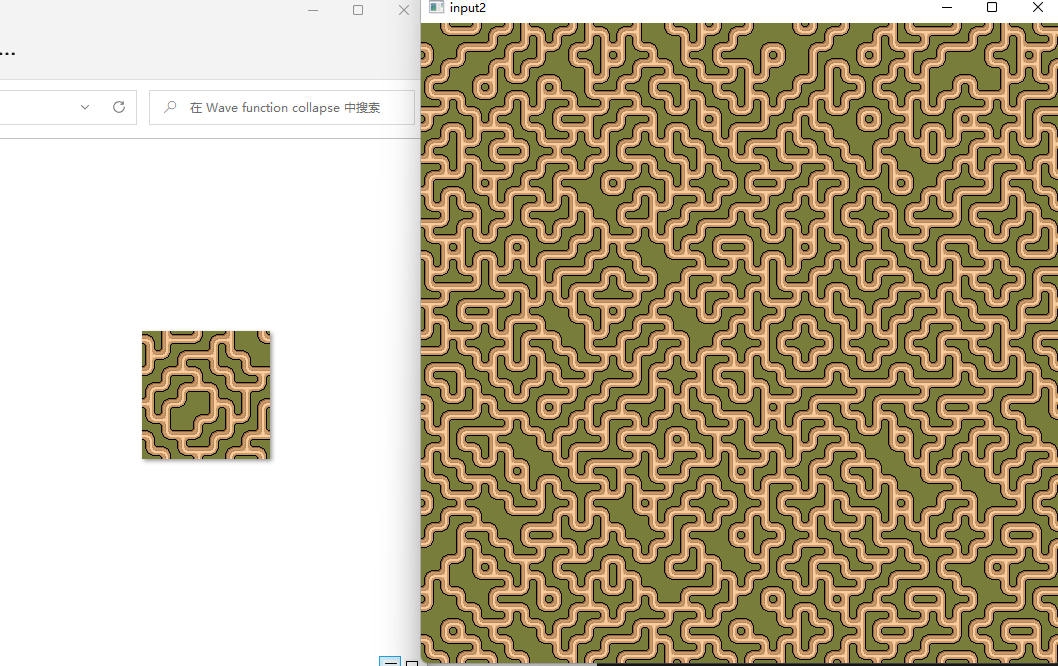
4.

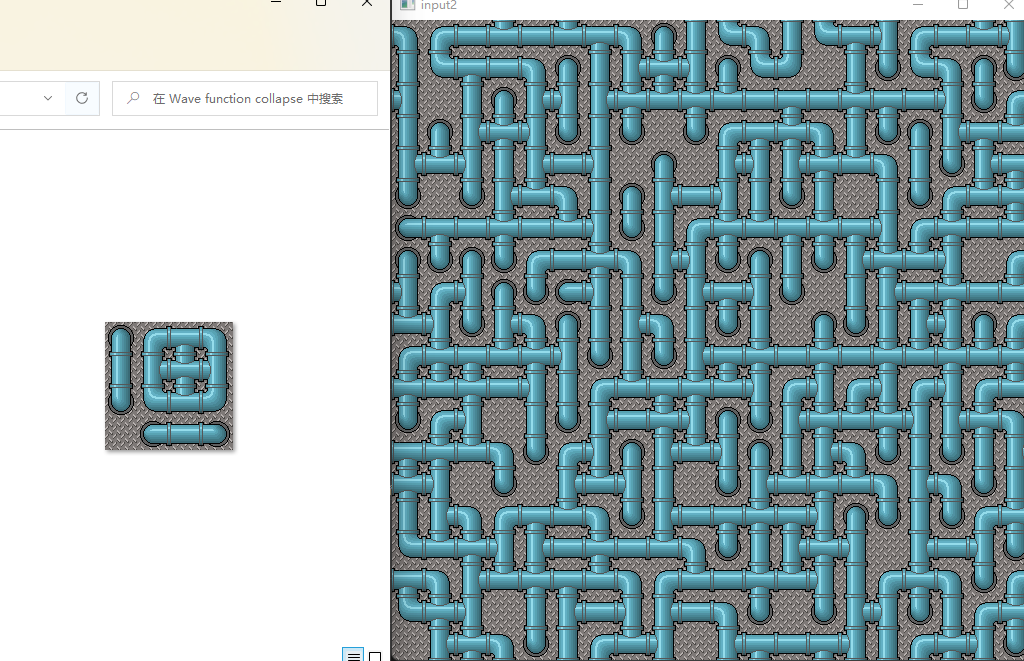
5.

二 , 复现过程

1. 截取图像的一小块区域

Mat src = imread(filename);
Mat s = src(Range(0, 31), Range(0, 31));          //截取(0,0)到(31,31)的矩形区域
Mat ans = Mat::zeros(Size(512,512),src.type());

2. 重复操作,截出所有图块

vector<Mat> elements;
    for (int i = 0; i < 4; i++)
    {
        for(int j = 0; j < 4; j++)
        {
            Mat s = src(Range(i * 32, i * 32 + 31), Range(j * 32, j * 32 + 31));
            elements.push_back(s);
        }
    }

3. 拷贝一个图块到输出

cv::Rect int2Rects(int x, int y)
{
    return cv::Rect(x * 32, y * 32,  31,  31);
}
int main(){
    //...
   Mat ans = Mat::zeros(Size(512,512),src.type());
   elements[0][0].copyTo(ans(int2Rects(1,1)));
   imshow("input2", ans);
}

4. 通过计算边界的均方根误差求出连通性

double calcRMS(vector<int>&Data)
{
    int Num = Data.size();
    double fSum = 0;
    for (int i = 0; i < Num; ++i)
    {
        fSum += Data[i] * Data[i];
    }
    return sqrt(fSum / Num);
}

vector<vector<vector<int>>> feasibility;
    for (int cur1 = 0;cur1<16;cur1++)
    {
        cout << endl;
        vector<vector<int>> temp2;
        for (int i = 0; i < 4; i++)     //edges
        {
            vector<int> temp3;
            cout << endl;
            for (int cur2 = 0; cur2 < 16; cur2++)
            {
                if (cur2 == cur1)continue;
                vector<int> data_1;
                for (int cur3 = 0; cur3 < 31; cur3++)
                {
                    int duiying = 0;
                    if (i == 0)duiying = 1;
                    if (i == 1)duiying = 0;
                    if (i == 2)duiying = 3;
                    if (i == 3)duiying = 2;
                    data_1.push_back(datas[cur1][i][cur3] - datas[cur2][duiying][cur3]); 
                }
                double _RMS = calcRMS(data_1);
                cout << _RMS<<" ' ";
                if (_RMS < 5.0f)
                {
                    temp3.push_back(cur2);
                }
            }
            temp2.push_back(temp3);
        }
        feasibility.push_back(temp2);
    }

5. 根据上面求出的连通性, 求出每个图块的熵, 并填充当前熵最小的图块. 重复直到每个图块都被确定

int count_V(vector<int>& v)
{
    int count = 0;
    for (auto i : v)
    {
        if (i == 16)
            count++;
    }
    return count;
}

vector<int> vectors_intersection(vector<int> v1, vector<int> v2) {
    vector<int> v;
    sort(v1.begin(), v1.end());
    sort(v2.begin(), v2.end());
    set_intersection(v1.begin(), v1.end(), v2.begin(), v2.end(), back_inserter(v));//求交集 
    return v;
}



vector<int> result(LEN__* LEN__, 16);
    int vaild = 0;
    while (count_V(result)>0)
    {
        if (vaild > 1000)break;
        auto last = count_V(result);
        int min = LEN__+1;
        int minx = -1, miny = -1,minid = -1;
        int mindata = -1;
        for (int x = 0; x < LEN__; x++)
        {
            for (int y = 0; y < LEN__; y++)
            {
                int id = x * LEN__ + y;
                if (result[id] == 16)
                    cout << "x:" << x << "y:" << y<<"last:"<<last << endl;
                if (result[id] == 16)
                {
                    vector<int> probably,top,down,left,right;
                    vector<vector<int>> edges;
                    if (x == 0) top = all_accept;
                    else top = feasibility[(result[id - LEN__])][1]; 
                    if (x == LEN__-1) down = all_accept;
                    else down = feasibility[result[id + LEN__]][0];
                    if (y == 0)left = all_accept;
                    else left = feasibility [result[id - 1]][3];
                    if (y == LEN__-1)right = all_accept;
                    else right = feasibility [result[id + 1]][2];
                    probably = top;
                    probably = vectors_intersection(probably, down);
                    probably = vectors_intersection(probably, left);
                    probably = vectors_intersection(probably, right);

                    if (probably.size() == 0)
                    {
                        vaild++;
                    }
                    else
                    {
                        if (probably.size() < min)
                        {
                            //cout << probably.size()<<" "<<id<<probably[0] << endl;
                            min = probably.size();
                            minx = x;
                            miny = y;
                            minid = id;
                            mindata = probably[rand() % ((probably.size() == 1) ? 1 : ((probably.size() - 1)))];
                        }
                        else
                        {
                            cout << probably.size() << endl;
                        }
                    }
                }
                else
                {
                    continue;
                }
            }
        }
        if(minx>=0)
        {

            vaild = 0;
            elements[mindata].copyTo(ans(int2Rects(miny, minx)));
            result[minid] = mindata;
            imshow("input2", ans);
            waitKey(20);
            //destroyAllWindows();
        }
    }